レンズの性能指標である収差を概念的に説明するシリーズ記事です。
収差の中でも本項では「歪曲収差」について図やシミュレーションを使い簡単でわかりやすく紹介します。
なお、他の収差に関する解説記事をお探しの場合は、以下をご参照ください。
収差と歪曲収差
まず、収差とは理想的な結像関係とのズレを示す指標です。
カメラのレンズは、「被写体」から放たれる光を正確に撮像面(フィルムやCMOS)へ「集光」させることを目的としています。
しかし、正確に集光させることは難しく、どうしてもズレるそのわずかな量を「収差」と呼びます。
この収差は、特徴ごとに分類されそれぞれに名称が付けられています。
今回は「歪曲収差」についての解説になります。
過去に説明した球面収差や軸上色収差は、写真の中心の性能を表す収差でしたが、歪曲収差は写真の周辺部分の収差となります。
なお歪曲収差は、収差の中で唯一名称からイメージのわかる収差ではないでしょうか?
本項では、できるだけ簡単な概念として理解できるように「歪曲収差」と供に、混同されやすい「パースペクティブ(遠近感)」についても解説したいと思います。
まずは想像してみましょう
とある名城を訪れると、極めて美しい石垣があり、それを撮影しようとします。
例えばこんな石垣です。

直角に切り出された石が寸分たがわず、隙間もなく並んでいます。
こんな美しい石垣があればつい撮影してしまうものです。
しかし、写った写真を見てみると、あるレンズではこのようになりました。

周辺部が縮んだように撮影されています。
また、他のレンズでは異なる写り方をしています。
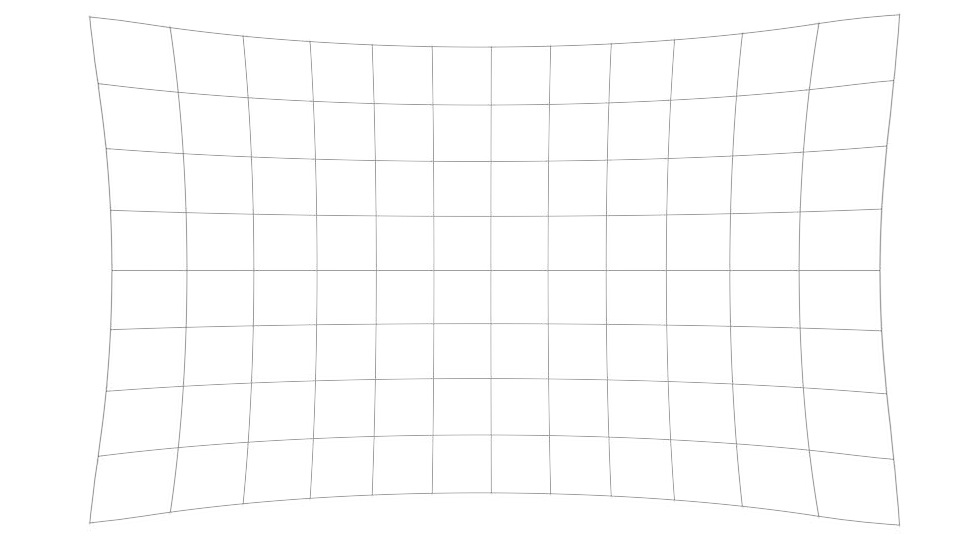
今度は周辺部が引き延ばされたように写っています。
このような歪みを「歪曲収差」と呼びます。
樽型と糸巻き型
先ほどの歪曲収差の2種類の形には名前が付けられています。

このように中心に対して周辺が縮む形を「樽型」と言います。
もう一方は
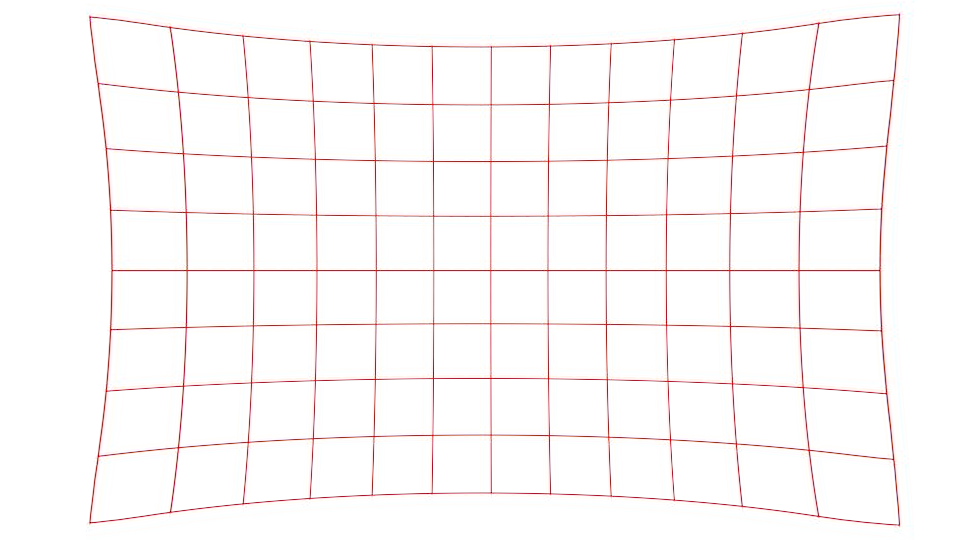
周辺が伸びた形を「糸巻き型」と言います。
樽型は、広角レンズによく見られる収差で、糸巻き型は望遠レンズで発生しやすいですが、よく見かけるのは樽型でしょう。
まずは1枚のレンズで考える
当ブログでのレンズ分析記事で毎度登場する光路図において、歪曲収差がどのように見えるのかシミュレーションを使って説明します。
先ほど例に挙げた、「石垣を写す」様子は、光路図としては下図のように表現されます。
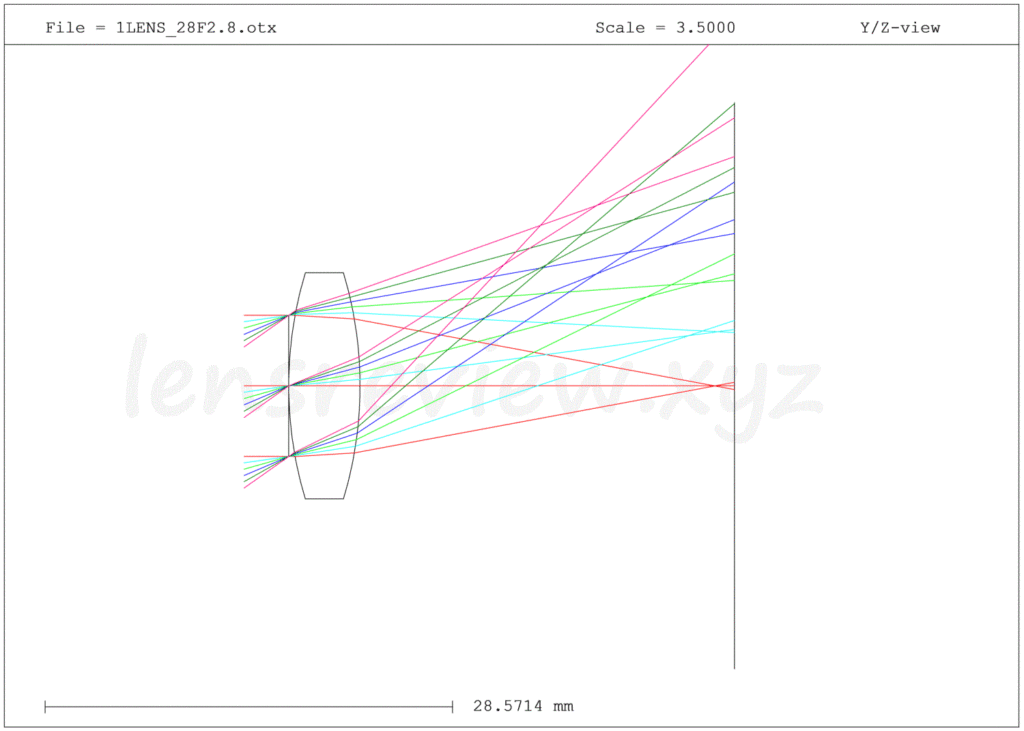
今回のレンズは、たった1枚で構成された「焦点距離28mm Fno2.8」の広角レンズを準備しました。
たった1枚なので収差が大きく、光路がわかりづらいので、各光線束において絞り中心を通る光線のみ描画します。

だいぶすっきりと見やすくなりました。
この状態ですでに歪曲収が発生しており、その影響が見えています。
その現象とは、光路図をよく見ると撮像素子の高い位置(画面の隅にあたる位置)に光線が当たっていません。
これは歪曲収差によって画面中心側へ光線が縮んでしまっている事を示しています。
それでは「歪曲収差が無い場合の光線経路」と「歪曲収差がある場合」を重ねて表示してみます。
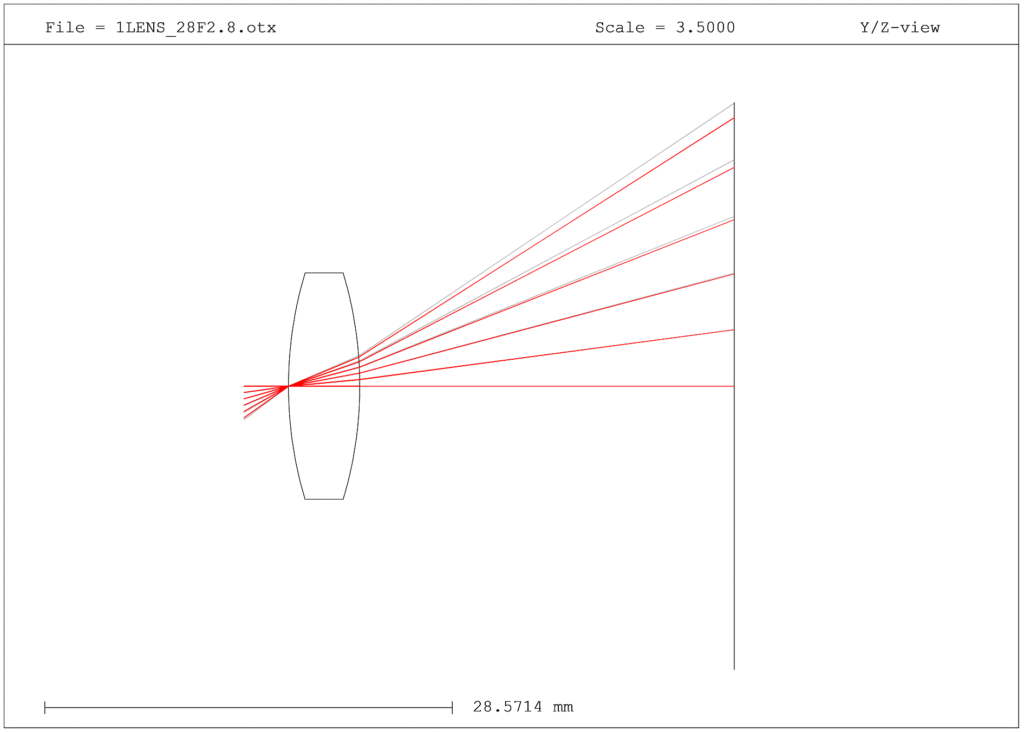
グレーの線は収差が無かった場合、赤線は収差を考慮した場合の光線経路です。
赤い光線は全体に画面の中心寄りにずれていることがわかります。
歪曲収差の概念図
これに補助線を追加し、収差図の概念を説明したのが以下の図になります。
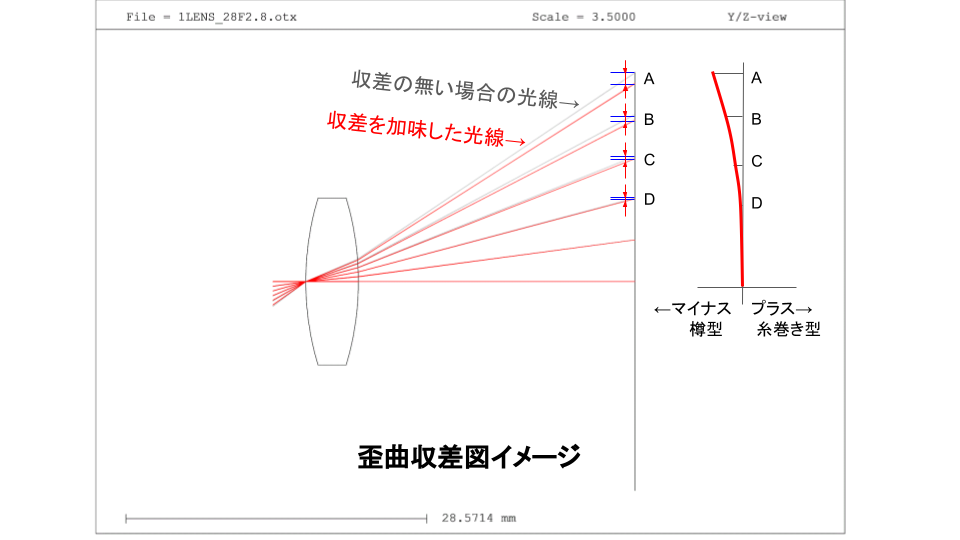
この例の場合、収差を考慮した真実の経路(赤線)は、収差を無視したグレーの線よりも画面中央寄りにずれています。
これを収差図として表現するとマイナス側へ倒れた形になり、「樽型形状」に写ることを示唆しています。
逆にプラス側へグラフが倒れる場合は、「糸巻き型形状」であることを示します。
収差図で表現
さて、いつもの分析記事でご紹介する収差図で表現してみましょう。
普段のレンズ分析記事では左から「球面収差」「像面湾曲」「歪曲収差」の順で並べて表示しております。

なお、通常のレンズ分析記事における縦収差図の球面収差や像面湾曲の横軸スケールは±0.5mmですが、今回の1枚レンズは収差量があまりにも大きく横軸スケールを±10mmとしています。通常の20倍となっていますのでご注意ください。
なお、歪曲収差のスケールは通常の分析記事と同じく±5%です。
さて今回のテーマとなります歪曲収差図を見ると、グラフの上端部では5%を超えており、およそ8%程度発生しているようです。
一般的に安いズームレンズの広角端では、歪曲収差が5%程度ありますが、8%と言う数値はまず見ることの無いほどの大きさです。
単焦点レンズであれば、手ごろな価格のレンズでも3%程度に抑えられるのが一般的です。
たった1枚のレンズでは歪曲収差が大きいことがおわかりいただけたでしょうか。
パースペクティブ
よく歪曲収差と混同されるのが「パースペクティブ(遠近感)」です。
例えば「広角レンズは、パースがキツイ」などと表現しているのを聞いたことがあるのではないでしょうか?
パースペクティブとは、日本語では遠近感の事で、簡単に言えば「遠くの物は小さく見える」現象です。
これをレンズによる歪と勘違いされてしまう方が多いのです。
パースペクティブについて簡単に図示してみます。
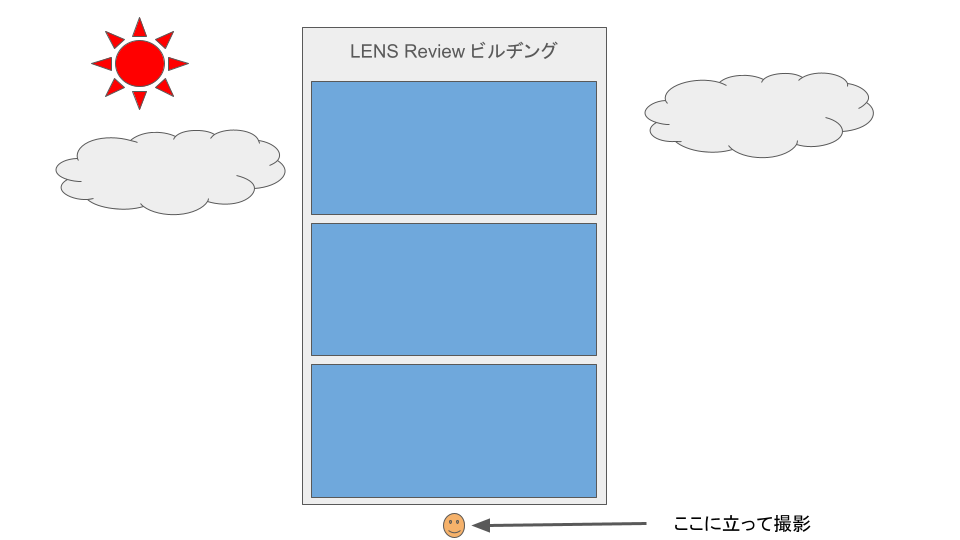
あるビルのふもとから見上げるように写真を撮る事を想像してください。
(これは夢の自社ビルじゃぁないですか…)
実際の写真はこのような写りになるでしょう。

ふもとから撮影するとビルの頂上側は小さくすぼんだように写ります。
これは「遠くの物は小さく見える」遠近感によるものでレンズの収差とは関係がありません。
広角レンズほどこの現象が強くなります。
この時、広角レンズほど歪曲収差の補正が難しいこともあり、歪曲収差とパースペクティブが混同されてしまう事が多いように感じます。
よく混同してしまう代表的な例は、広角レンズで人物撮影をすると、妙に「手足が伸びた」「顔を小さく写る」などの違和感が出ることが多く、これを歪曲収差だと勘違いされることがあります。
撮影の条件による部分もあり完全に分離はできませんが、経験上は上記の例ならパースペクティブによる違和感です。
なぜなら、広角レンズというのは人の目を大きく超えた範囲が写るためパースペクティブがより誇張されます。
そのため、人の目の感覚よりも遠くの物がずっと小さく写るために「手足が長すぎる」などの違和感となるのです。
ただし、広角レンズの楽しみ方のひとつでもありますから「使いよう」であることは説明不要ですね。
デジタル歪曲補正
歪曲収差は、2次元平面上の幾何学的な現象としてとらえる事ができるため、デジタル処理によって補正することが容易です。
デジタル処理をイメージ的に表現すれば、例えば樽型の収差なら周辺部を引き延ばすような処理をすれば元に戻すことができると言うわけです。
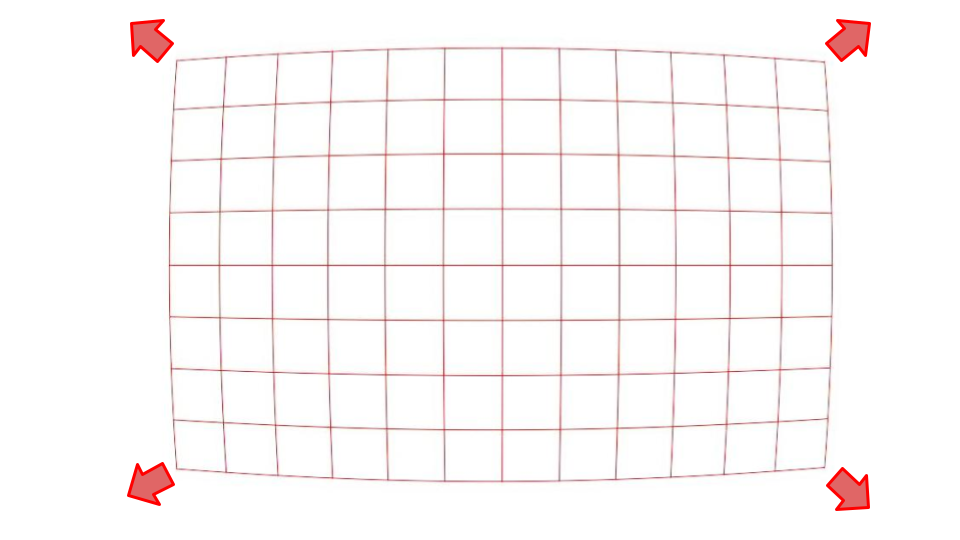
最近の交換レンズの中ではデジタル処理による歪曲補正を施すことを前提とした物が増えているようです。
例えば、過去に分析を行ったSIGMA 85mm F1.4ではメーカーが公式にデジタル処理していることを公言しています。
デジタル処理は、メーカーにより作動は様々ですが、カメラ内部で撮影と同時処理することもできたり、現像ソフトによる後処理も可能です。
私が使用している画像現像処理ソフトSILKYPIXでは、歪曲収差の補正機能があり、好きなように補正処理することが可能です。
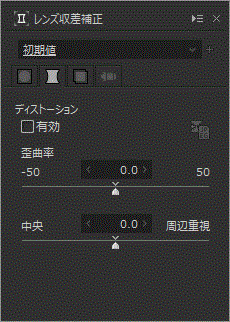
こちらの操作パネルは、SILKYPIXの歪曲収差(ディストーション)の補正画面です。
SILKYPIXについて、簡単にご紹介する記事も作成しておりますので合わせてご覧いただけると幸いです。
関連記事:SILKYPIX
歪曲収差を補正する
先ほどまでは1枚のレンズでの説明でしたが、現実的にはこんなに広角でFno明るいレンズならばたくさんの枚数で構成されています。
ここでは改めて歪曲収差の補正されたレンズの特性を見てみましょう。
先ほどはたった1枚で構成された28mm F2.8レンズの収差を紹介しました。
これまでの歪曲収差のグラフスケールで広角レンズの定番レトロタイプの6枚構成レンズの歪曲収差がどうなるか下図に示します。
光路図
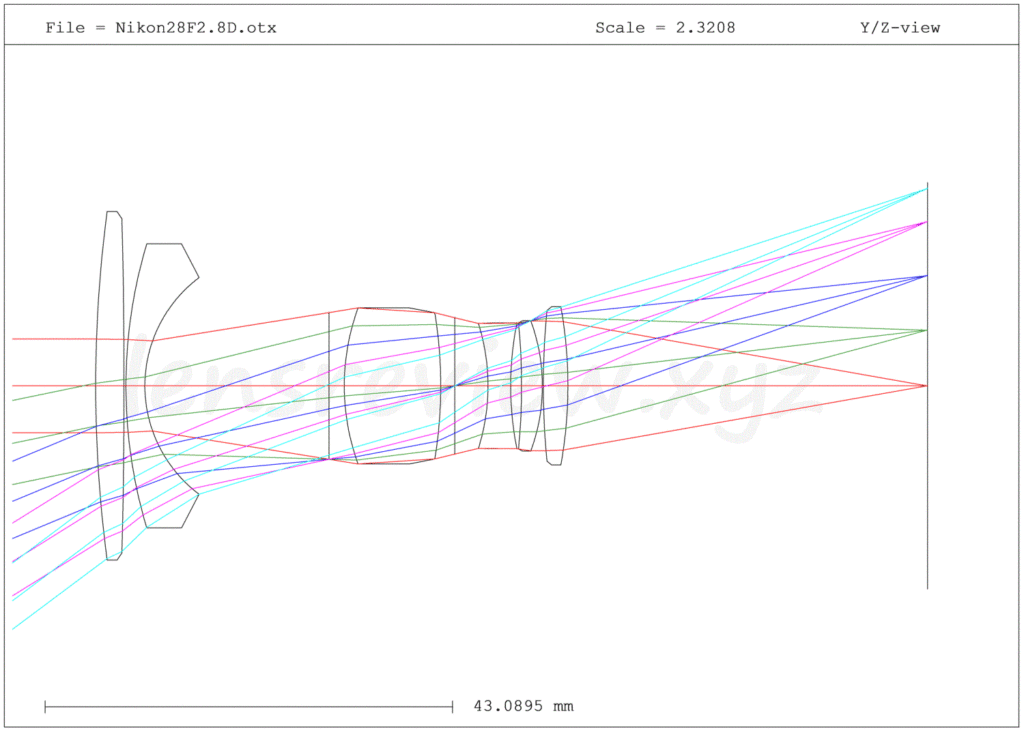
こちらの光路図は、過去に分析したNIKON NIKKOR 28mm F2.8Dとなります。広角レンズの定番たるレトロタイプでいかんとも懐かしい姿をしています。
歪曲収差の補正に効果的な非球面レンズは非採用となっています。
縦収差

最初の1枚構成レンズの横軸スケールに合わせ、球面収差や像面湾曲のグラフは通常の20倍サイズでグラフを作っています。
歪曲収差のスケールは通常と同じ±5%です。
レンズ構成枚数も少なく、懐かしいぐらい控えめで清楚なレンズ構成でありますが、歪曲収差は最大でも3%程度にしっかりと補正されています。
デジタル処理の無いフィルム時代の広角レンズは、このように若干の歪曲収差が樽型に残っていることが普通でしたので、私としてはこの程度の歪曲収差が残っている方が広角レンズらしい写りで味があり好ましいと思います。
最近のデジタル処理を駆使した高画質化は最初は感動しますが飽きも早く来てしまいますね…
さて、いつものグラフスケールでご覧になりたい方は元の記事をご確認ください。
まとめ
わずか一言で説明すれば「歪曲収差とは画面周辺部の伸び・縮みしたような歪」です。
きっと歪曲収差をご理解いただけた事で当ブログが20倍楽しめるようになったと思います。
なお、他の収差に関する解説記事をお探しの場合は、以下をご参照ください。
さらに深く光学に関して学びたい方へおススメしたい書籍の紹介はこちらです。
関連記事:光学設計者がおススメする「光学の入門書」
「もっと初歩から…」と思われた方は、実質無料でも読めるこちらを参考にしてはいかがでしょうか?
関連記事:カメラとレンズの「しくみ」がわかる本




