レンズの性能指標である収差を概念的に説明するシリーズ記事です。
収差の中でも本項では「球面収差」について図やシミュレーションを使い簡単でわかりやすく紹介します。
なお、他の収差に関する解説記事をお探しの場合は、以下をご参照ください。
収差と球面収差
まず、収差とはレンズの性能指標を表す言葉で、理想的な結像関係とのズレ、すなわち「光の集まり具合」を示す指標です。
カメラのレンズは、「被写体」から放たれる光を正確に撮像面(フィルム/COMS)へ「集光」させることを目的としています。
しかし、正確に集光させることは難しく、どうしてもズレるそのわずかな誤差量を「収差」と呼びます。
この収差は、特徴ごとに分類されそれぞれに名称が付けられています。
この中で、少しレンズに詳しい方ならば必ず耳にしたことのあるのが「球面収差」でしょう。
なぜなら「球面収差」とは最も基本の収差だからです。
まず「球面収差」と聞くと、難解な数式をイメージしてしまうかもしれません。
本項では、できるだけ簡単な概念として理解できるように「球面収差」について解説したいと思います。
まさか、コダックのデジカメが爆売れする世界が来るなんて
まずは想像してみましょう
真っ暗な空に、たったひとつ星があり、この星を「写真のド真ん中へ写そう」とした、とします。

この星は何光年も先の遥か彼方にあるものですから、地球上で写真に写すとしたら「極小さな光の点」に写ることが理想の写真であることは感覚的にわかるはずです。(空気の揺らぎなどは無視します)

しかし、残念な事にレンズ性能の影響によっては、理想的な小さな点に結像できず、少しぼやけた点になってしまうことがあります。
この理想からのズレが「収差」と言われる量で、写真のド真ん中におけるボケ量が「球面収差」と言われる指標値です。
なぜならレンズは丸いから
光を集める役割を持つレンズは基本的には球を切り出した形状をしています。(レンズは丸い)
そのためレンズ中心ほど光を集める性質が対称(均一)となり、画面全域の中でド真ん中の集光度が最も良くなります。
よって、ド真ん中(中心)の性能を見れば高性能なレンズかすぐにわかると言えます。
逆に言えば、「ド真ん中の性能が悪いようでは高性能は望めない」わけです。
そのため、ド真ん中の性能を表す「球面収差」は全ての収差の基本であり最も重要とされるのです。
まずは1枚のレンズで考える
当ブログでのレンズ分析において掲示している光路図において、球面収差がどのように見えるのかシミュレーションを使って説明します。
先ほど例に挙げた、「遥か彼方の星を画面のド真ん中に写す」様子は、光路図としては下図のように表現されます。
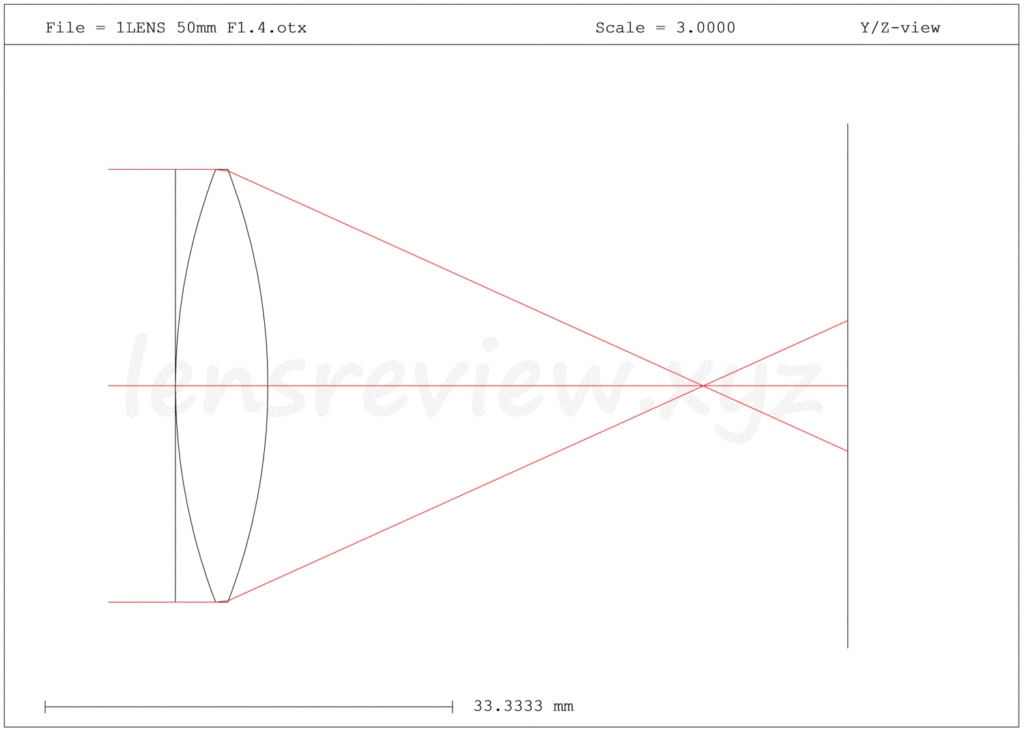
上図はたった1枚の球面レンズで構成された50mm F1.4仕様のレンズです。
雑貨店で売られているような安価な虫メガネをカメラ用のレンズとして使う様子を想像してください。
まず、レンズを通過する光の様子を観察してみましょう。(赤線)
星のように超遠距離の光源から放たれた光(赤線)が、地球上のレンズへ当たるころにはレンズに対して略垂直に入射するような位置関係となります。
レンズを通過した光は、図の右側にある撮像面(フィルムやCMOSに相当)に向かって進み、撮像素子の手前でクロスしています。
なんとも意味深です。
なお、被写体となる星は、画面の左方向で遥か数光年ほどにあり、描画することが困難なので割愛しています。
この超遠距離からの光を集光している様子を「無限光(又は平行光)を集光する」などと表現します。
一般に、カメラのレンズを収差値で表す場合、このように遠い星を写すような撮影距離の状態で収差値を表すことが慣例となっています。
また、光路図の基礎については別記事を準備してあります。そちらの解説も合わせてお読みいただけると理解がより深まるでしょう。
関連記事:光路図を図解
さらに少し詳しく光路図を見てみましょう。
いつもの光路図の描画方法の場合、レンズの外径すれすれを通る光だけ描画しているので、一見すると光が1点に集光しているように見えます。
しかし実際のところ、光は無尽蔵に細かい線(シャワー)が降り注ぐかのように、たくさん虫メガネレンズを通過しています。
そこで、描画する光の本数を増やしてみましょう。
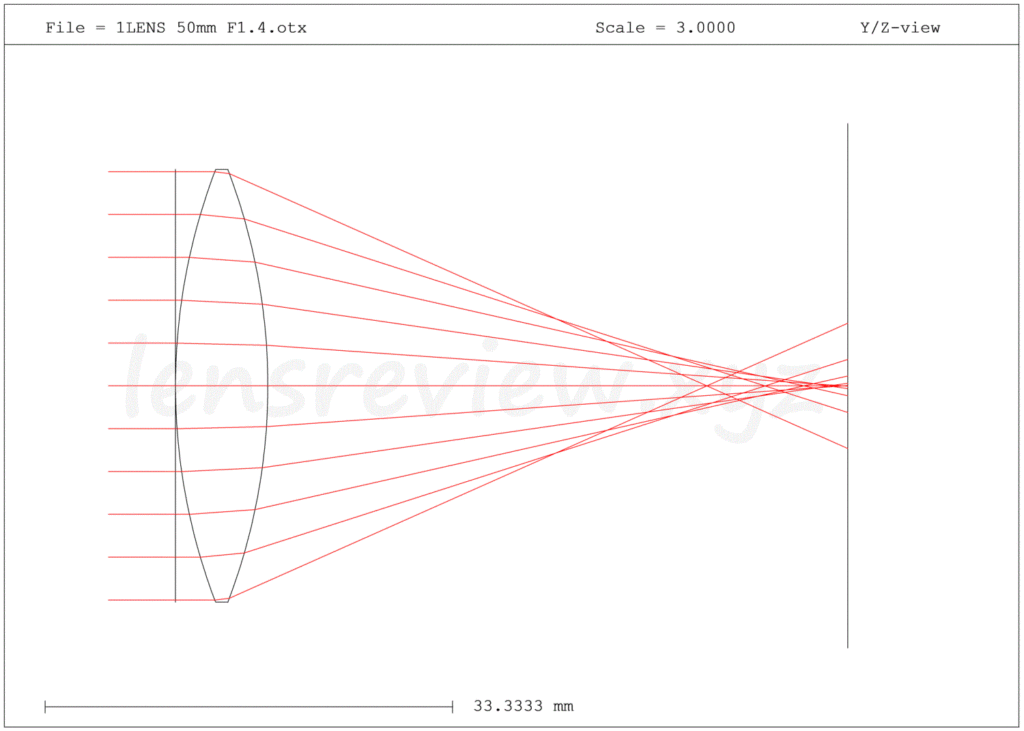
上図は、光の本数を増やして表現したものです。本来ならば、無尽蔵にあるのですが、書ききれないので見やすい程度の本数に抑えています。
さて、光の集光する撮像素子(フィルム面)あたりを見てみると完全な点にはなっていません。
レンズの「中心部を通る光」と「外周部を通る光」は異なる位置に集光することがわかります。
すなわち、レンズの口径(Fno)も関係しますが、たった1枚の球面レンズでは「球面収差」の影響で理想的な点に集光することができないのです。
収差図で表現
ようやくここから、当ブログのレンズ分析記事に出る球面収差図の形式でこの1枚のレンズを表現してみます。
さて、いつもの表記では下図のようになります。
縦収差
球面収差、像面湾曲、歪曲収差のグラフ
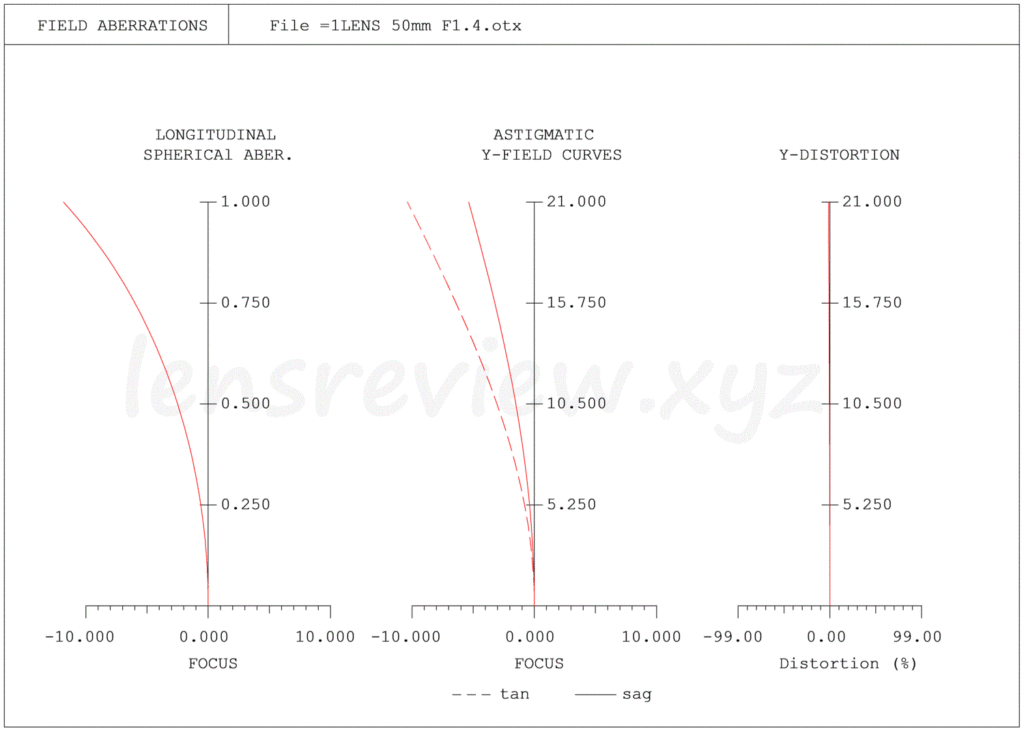
レンズ分析記事では「縦収差」の中のひとつとして球面収差のグラフを示しています。
当ブログでも記事内における最初のグラフとして位置するように球面収差図を配置しています。最も重要なグラフであると位置づけているからです。
縦収差と球面収差の配置の解説図はこちらです。
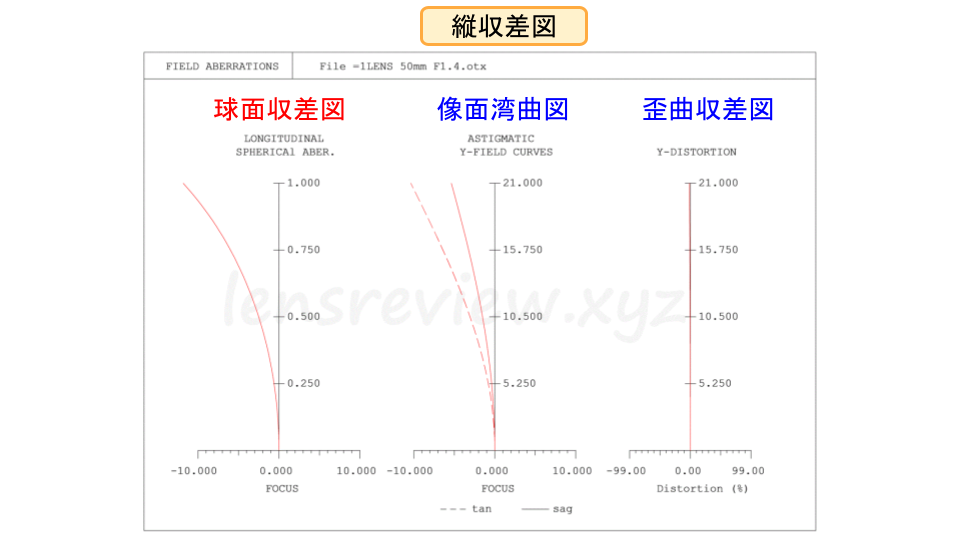
いつのものレンズ分析記事での収差図の横軸スケールは±0.5mmですが、今回の1枚レンズは収差量があまりにも大きく横軸スケールを±10mmとしています。通常の20倍となっていますのでご注意ください。
さて、この球面収差図の縦軸/横軸はどのような意味でしょうか。記事はまだまだ続きます。
図解:球面収差
先ほどの光路図と球面収差をもう少し簡単に図解してみます。
光路図と球面収差の関係を簡易的に表現すると下図のような関係になります。
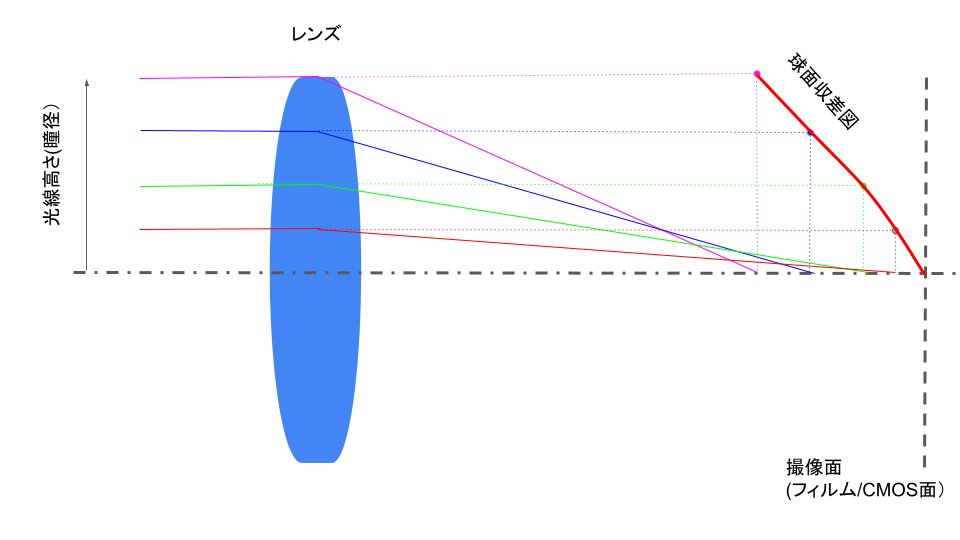
球面収差図の構成を解説するとグラフを構成する縦軸と横軸は
・横軸:光ごとの集光位置(ピントずれ)
・縦軸:光線の入射位置(高さ)
を示しています。
球面収差グラフの縦軸/横軸の関係性がおわかりでしょうか?
このグラフからいくつもの事柄が読み取れます。
例えば、球面収差が大きいレンズはピントがずれているように見えるがピント位置が無数にあり、1点では表現できない、とか。
Fnoの明るいレンズとは光線高さが高い、すなわち球面収差の縦軸が長い、それはFnoが明るいほど球面収差が増大する。そんな事も予見できますね。
関連記事:Fnoとレンズ径
球面収差を補正する
先ほどまでは1枚のレンズでの説明でしたが、現実的にはこんなにFnoの明るい光学系ならばたくさんのレンズ枚数で構成されています。
ここでは改めて球面収差の補正されたレンズの特性を見てみましょう。
先ほどはたった1枚で構成された50mm F1.4レンズの収差を紹介しました。
同じ球面収差のグラフスケールでダブルガウスタイプの7枚構成レンズの球面収差がどうなるか下図に示します。
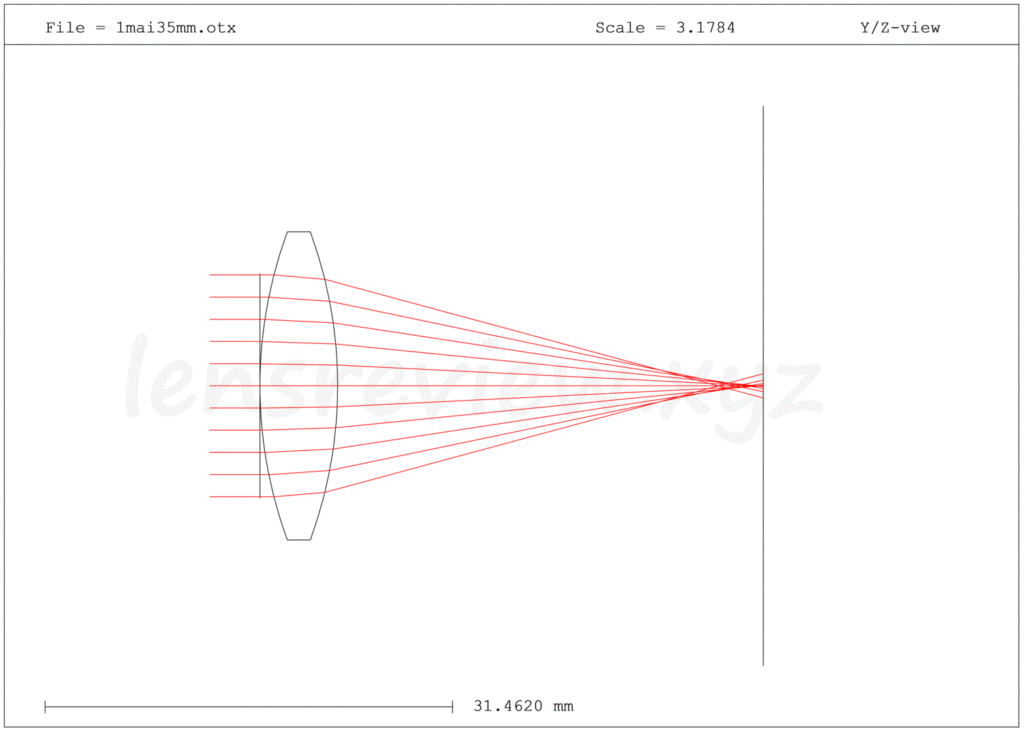
光路図

光路図で見る構成は上図のようになっています。
このレンズは、過去に分析したNIKON NIKKOR 50mm f1.4Dです。
縦収差
球面収差、像面湾曲、歪曲収差
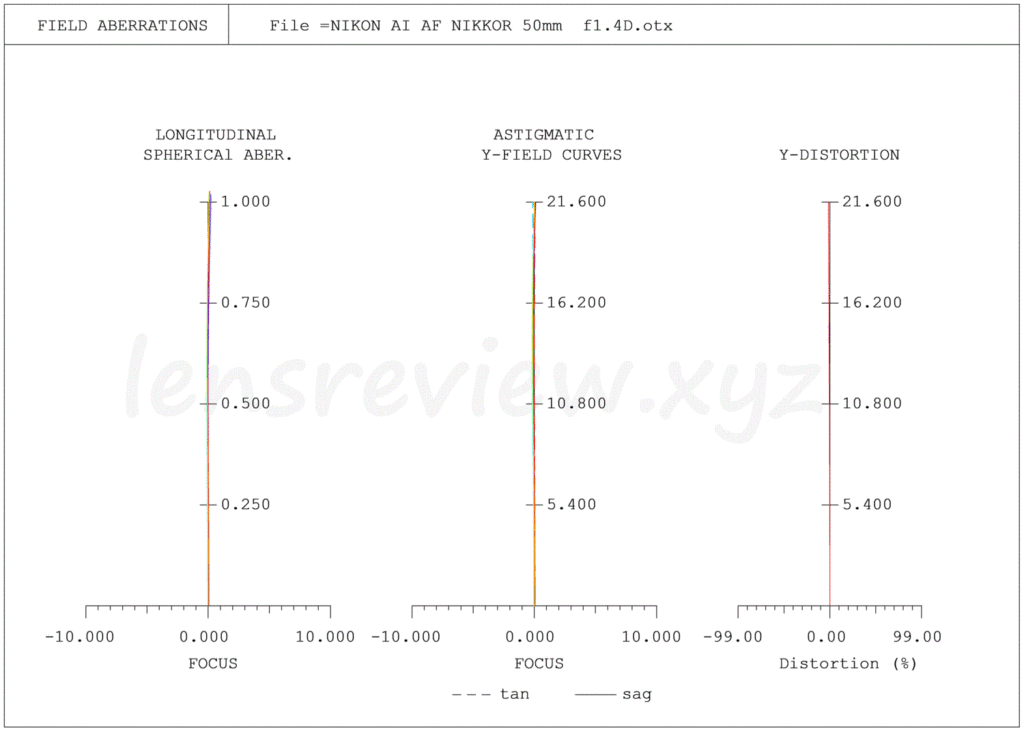
最初の1枚構成レンズの横軸スケールに合わせ、通常の20倍サイズでグラフを作っています。
球面収差図を見ると略直線で表示する必要性があったのかすら疑問もありますが、このレンズは最も安価なクラスの製品ですが、人類の英知の結晶たるダブルガウスタイプレンズ特性を見事に活用し、極めて少数のレンズで収差補正が成されている凄みがご理解いただけるのではないでしょうか?
いつものグラフスケールでご覧になりたい方は元の記事をご確認ください。
関連記事:分析NIKON NIKKOR 50mm f1.4D
まとめ
わずか一言で説明すれば「球面収差とは画面のド真ん中における像のボケ具合」です。
きっと球面収差をご理解いただけた事で当ブログが20倍楽しめるようになったと思います。
レンズレビュー激推し、カメラバッグ
なお、他の収差に関する解説記事をお探しの場合は、以下をご参照ください。
さらに深く光学に関して学びたい方へおススメしたい書籍の紹介はこちらです。
関連記事:光学設計者がおススメする「光学の入門書」
「もっと初歩から…」と思われた方は、実質無料でも読めるこちらを参考にしてはいかがでしょうか?
関連記事:カメラとレンズの「しくみ」がわかる本





